Matematik FP10
Til dette opgavesæt hører en regnearksfil til opgave 4 og svarark til opgave 3, 6 og 7
Tirsdag den 3. maj 2022
kl. 14.00-18.00
Kære elev
Prøven består af 8 opgaver. Du har 4 timer til at løse dem.
Ved hver opgave står der, hvor mange point den højst kan give.
Prøven kan i alt højst give 72 point. Du bestemmer selv, hvilken rækkefølge du laver opgaverne i, og hvor lang tid du vil bruge på hver af dem.
Det er vigtigt, at du begrunder dine svar i alle opgaver.
Det betyder, at du i hver opgave skal vise eller forklare, hvordan du er nået frem til dit svar. Du kan fx begrunde dit svar med tekst, beregninger og/eller tegninger.
En del af de point, du kan få i hver opgave, kommer fra dine begrundelser. I de fleste opgaver kan du ikke få det højeste antal point, hvis du ikke begrunder dit svar, selv om dine resultater er rigtige.
I nogle af opgaverne skal du beregne et antal eller en størrelse. I andre opgaver skal du vise, hvordan du finder frem til et bestemt resultat eller afgøre, om en påstand er sand eller falsk.
Der er også opgaver, hvor du skal løse et matematisk problem ved at undersøge. I disse opgaver forventer vi ikke, at du på forhånd kender en metode, du kan bruge til at løse problemet. Ordet ’undersøg’ signalerer, at du selv skal finde på en god måde at løse problemet på ved at bruge matematik, du kender.
God arbejdslyst.
Styrelsen for Undervisning og Kvalitet
Prøven består af 8 opgaver. Du har 4 timer til at løse dem.
Ved hver opgave står der, hvor mange point den højst kan give.
Prøven kan i alt højst give 72 point. Du bestemmer selv, hvilken rækkefølge du laver opgaverne i, og hvor lang tid du vil bruge på hver af dem.
Det er vigtigt, at du begrunder dine svar i alle opgaver.
Det betyder, at du i hver opgave skal vise eller forklare, hvordan du er nået frem til dit svar. Du kan fx begrunde dit svar med tekst, beregninger og/eller tegninger.
En del af de point, du kan få i hver opgave, kommer fra dine begrundelser. I de fleste opgaver kan du ikke få det højeste antal point, hvis du ikke begrunder dit svar, selv om dine resultater er rigtige.
I nogle af opgaverne skal du beregne et antal eller en størrelse. I andre opgaver skal du vise, hvordan du finder frem til et bestemt resultat eller afgøre, om en påstand er sand eller falsk.
Der er også opgaver, hvor du skal løse et matematisk problem ved at undersøge. I disse opgaver forventer vi ikke, at du på forhånd kender en metode, du kan bruge til at løse problemet. Ordet ’undersøg’ signalerer, at du selv skal finde på en god måde at løse problemet på ved at bruge matematik, du kender.
God arbejdslyst.
Styrelsen for Undervisning og Kvalitet
1
Penge til mad
Opgave 1 giver højst 10 point|
Victoria er flyttet hjemmefra og har sin egen indkomst. Hendes indkomst er ca. 8800 kr. om måneden efter skat, og hun bruger ca. 1900 kr. af pengene på mad. |
|
| 1.1 |
Hvor mange penge om måneden har Victoria til andre ting end mad?
|
| 1.2 |
Hvor stor en procentdel af sin indkomst efter skat bruger Victoria på mad?
I 2019 brugte voksne danskere i gennemsnit ca. 12 % af deres penge på mad. |
| 1.3 |
Hvor mange penge skulle Victoria bruge på mad om måneden, hvis beløbet skulle udgøre 12 % af hendes indkomst efter skat?
|
| 1.4 |
Hvor stor en indkomst efter skat skulle Victoria have, hvis de 1900 kr., hun bruger på mad, skulle udgøre 12 % af beløbet?
|
 Foto: Opgavekommissionen i matematik
Foto: Opgavekommissionen i matematik
2
Pizzaer i to forskellige størrelser
Opgave 2 giver højst 8 point|
På et pizzeria kan Victoria købe pizzaer i to forskellige størrelser. Tegningen herunder viser priser og mål på pizzaerne.
Pizzaerne har form som cirkler, når man ser dem fra oven. |

|
| 2.1 |
Du skal vise, at arealet af den lille cirkel er ca. 700 cm2.
|
| 2.2 |
Får Victoria mest pizza ved at købe 2 små eller 1 stor pizza?
Pizzeriaets ejer overvejer at ændre på den store pizzas størrelse, så man får lige meget for pengene, uanset om man køber den store eller den lille pizza. |
| 2.3 |
Undersøg, hvilken diameter den store pizza bør have, når den skal koste dobbelt så meget som den lille pizza.
|
 Foto: Opgavekommissionen i matematik
Foto: Opgavekommissionen i matematik
3
Kilokalorier og kilojoule
Opgave 3 giver højst 6 point|
I Danmark bruger vi kilokalorier (kcal) eller kilojoule (kJ) til at beskrive indholdet af energi i fødevarer. 1 kcal svarer cirka til 4,2 kJ.
|
| 3.1 |
Du skal vise sammenhængen mellem kilokalorier og kilojoule på tre forskellige måder:
|
4
Udvikling i løn og mælkepriser
Opgave 4 giver højst 8 point|
I år 1880 kostede 1 L mælk typisk 6 øre, og en faglært arbejder tjente typisk 27 øre i timen. |
|
| 4.1 |
Hvor mange liter mælk kunne en faglært arbejder købe for en timeløn i 1880?
På regnearket UDVIKLING_MAJ_2022 er der en tabel, der viser timelønnen for en faglært arbejder og prisen for 1 L mælk i perioden fra 1880 til 2004. |
| 4.2 |
Fremstil et diagram, der viser udviklingen i prisen for 1 L mælk.
|
| 4.3 |
Undersøg, hvordan forholdet mellem timelønnen og prisen for 1 L mælk har udviklet sig i perioden fra 1880 til 2004. Du kan begrunde din konklusion med beregninger eller med en graf i et koordinatsystem.
|
5
Madspild
Opgave 5 giver højst 10 point|
Eleverne på Kaspers efterskole vil gerne blive bedre til at undgå madspild. De har aftalt at veje deres madrester i tre uger. Diagrammet herunder viser vægten af 8 bordgruppers madrester i hele uge 1. |

|
| 5.1 |
Brug overslagsregning til at vise, at bordgruppernes madrester i alt vejede cirka 9 kg i uge 1.
|
| 5.2 |
Cirka hvor meget vejede bordgruppernes madrester i gennemsnit i uge 1?
I uge 2 havde bordgrupperne i gennemsnit ca. 1,0 kg madrester. En af grupperne havde kun ca. 0,5 kg madrester. |
| 5.3 |
Giv et eksempel på, hvor meget hver af de øvrige 7 bordgruppers madrester kan have vejet i uge 2.
Diagrammet herunder viser vægten af bordenes madrester i uge 3. |
| 5.4 |
Sammenlign diagrammet for uge 1 og 3 og vurder, om eleverne på efterskolen er blevet bedre til at undgå madspild på de 3 uger. Du skal begrunde dit svar med en kort tekst.
|
 Foto: Opgavekommissionen i matematik
Foto: Opgavekommissionen i matematik
6
En figurfølge
Opgave 6 giver højst 11 point
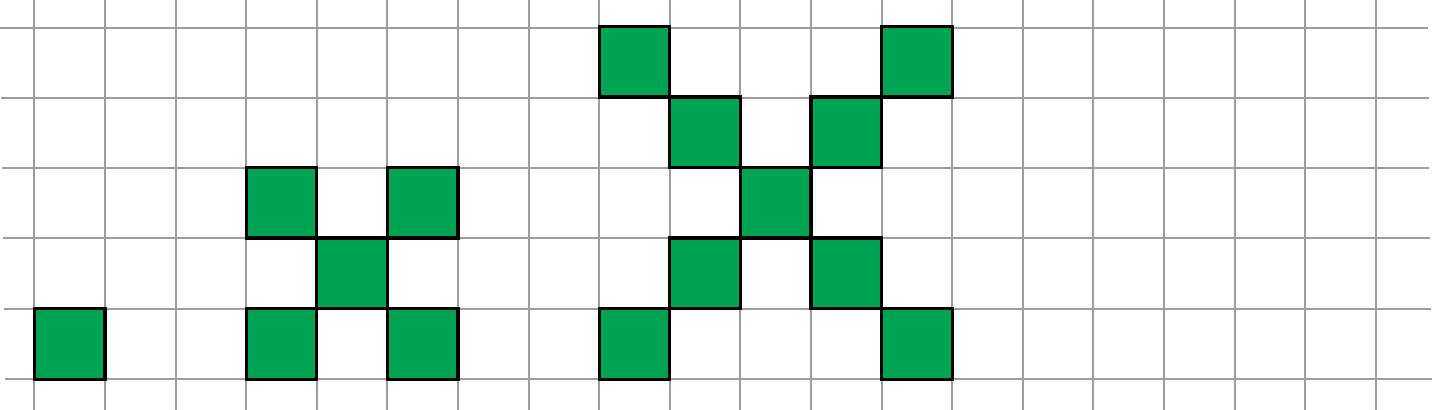
Figur 1, 2 og 3 er de første figurer i en figurfølge. Hver figur består af grønne kvadrater.
Figurfølgen fortsætter efter samme mønster, som den er begyndt. |
|||||||
| 6.1 |
Tegn figur 4 i figurfølgen. Brug evt. svararket.
|
||||||
| 6.2 |
Hvor mange kvadrater består figur 10 af?
|
||||||
| 6.3 |
Hvor mange kvadrater består figur n af?
|
||||||
| 6.4 |
Undersøg, om der i figurfølgen er en figur, der består af netop 100 kvadrater.
|
||||||
7
Regneruter
Opgave 7 giver højst 12 point|
I denne opgave kan du evt. bruge svararket.
Figuren i den blå ramme viser to udfyldte regneruter. Begge ruter begynder med tallet 3. Den øverste rute ender med 17, og den nederste ender med 32. |
|
| 7.1 |
Hvilke to tal vil de to regneruter i den blå ramme ende med, hvis de begynder med 4?
|
| 7.2 |
Hvilket tal skal de to regneruter i den blå ramme begynde med, hvis den øverste skal ende med 45 og den nederste med 60?
Hvis man begynder de to regneruter i den blå ramme med variablen a, vil den øverste regnerute ende med udtrykket a · 4 + 5. |
| 7.3 |
Hvilket udtryk vil den nederste regnerute i den blå ramme ende med, hvis man begynder med variablen a?
Figuren i den grønne ramme viser to andre regneruter. |
| 7.4 |
Bevis, at forskellen mellem de to tal, regneruterne i den grønne ramme ender med, er 12, uanset hvilket tal man begynder med.
|
8
Trekanter med bestemte mål
Opgave 8 giver højst 7 point|
Skitserne viser 5 trekanter. Nogle af trekanterne kan komme til at se ud på forskellige måder, når man tegner dem med de viste mål. Andre af trekanterne kan man slet ikke tegne, eller de kan kun komme til at se ud på én måde.
|
|
| 8.1 |
Undersøg for hver skitse, om man
Du kan fx begrunde dit svar med præcise tegninger. |